Método de Jacobi

En análisis numérico el método de Jacobi es un método iterativo, usado para resolver sistemas de ecuaciones lineales del tipo 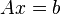$Ax=b$ . El algoritmo toma su nombre del matemático alemán Carl Gustav Jakob Jacobi. El método de Jacobi consiste en usar fórmulas como iteración de punto fijo.

La sucesión se construye descomponiendo la matriz del sistema $\mathbf{A}$ en la forma siguiente:

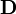$\mathbf{A} = \mathbf{D} + \mathbf{L} + \mathbf{U}$

donde

\mathbf{D}

, es una matriz diagonal.

\mathbf{L}

, es una matriz triangular inferior.

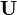\mathbf{U}

, es una matriz triangular superior.

Partiendo de 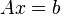$A x = b\,$ , podemos reescribir dicha ecuación como:

$\mathbf{D}x+\left( \mathbf{L}+\mathbf{U}\right)x = b$

Luego,

$x=\mathbf{D}^{-1} \left[ b-\left( \mathbf{L}+\mathbf{U} \right)x \right]$

Si a_ii ≠ 0 para cada i. Por la regla iterativa, la definición del Método de Jacobi puede ser expresado de la forma:

$x^{\left( k+1 \right)}=\mathbf{D}^{-1}\left[ b-\left( \mathbf{L}+\mathbf{U} \right)x^{(k)} \right]$

donde $k$ es el contador de iteración, Finalmente tenemos:

$x_{i}^{\left( k+1 \right)}=\frac{1}{a_{ii}}\left( b_{i} - \sum\limits_{j\ne i}{a_{ij}x_{j}^{\left( k \right)}} \right),i=1,2,3,...$

Cabe destacar que al calcular x_i^(k+1) se necesitan todos los elementos en x^(k), excepto el que tenga el mismo i. Por eso, al contrario que en el método Gauss-Seidel, no se puede sobreescribir x_i^(k) con x_i^(k+1), ya que su valor será necesario para el resto de los cálculos. Esta es la diferencia más significativa entre los métodos de Jacobi y Gauss-Seidel. La cantidad mínima de almacenamiento es de dos vectores de dimensión n, y será necesario realizar un copiado explícito.